Reference Graph
Construction and Merging for
Human Genomic Sequences


Want to sequence an individual human's DNA
Knowing how an individual's DNA differs from usual DNA can allow diagnosis of genetic disorders
Done by sequencing many short reads
Reads aligned to reference to find individual's variations
Too many wrong assembly possibilities without reference










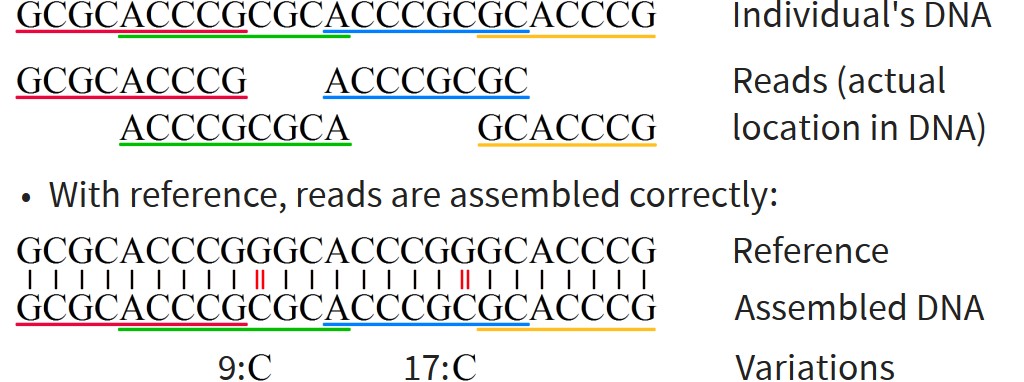
Graph reference lets us make better use of known information than reference string
Graph corresponds to several references with some similarities and some differences

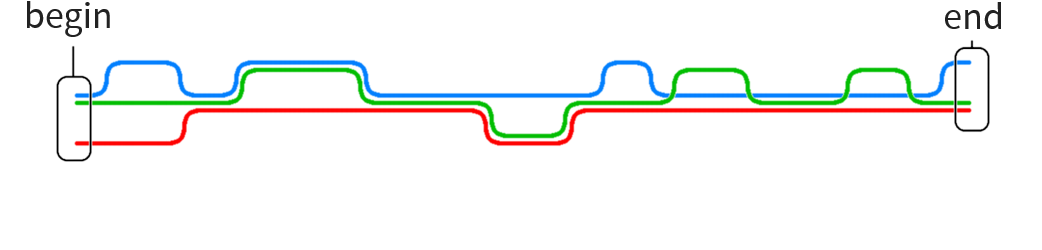
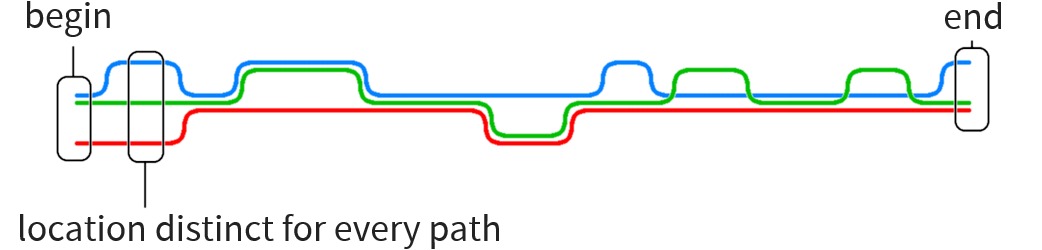

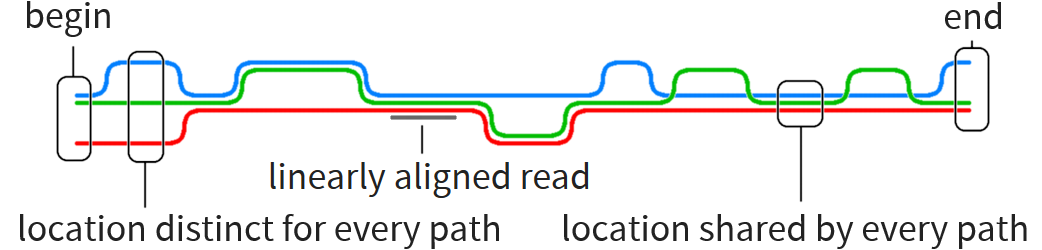
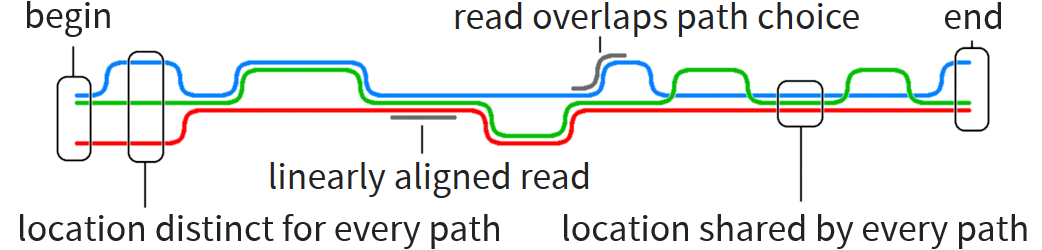
Particular problem motivating this thesis:
Construct human reference graph
Current implementations for graph generation cannot deal with graphs of such size
Our approach: use human reference string and add local graphs in various positions without having to encode the entire reference as graph
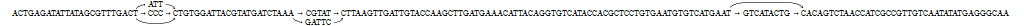
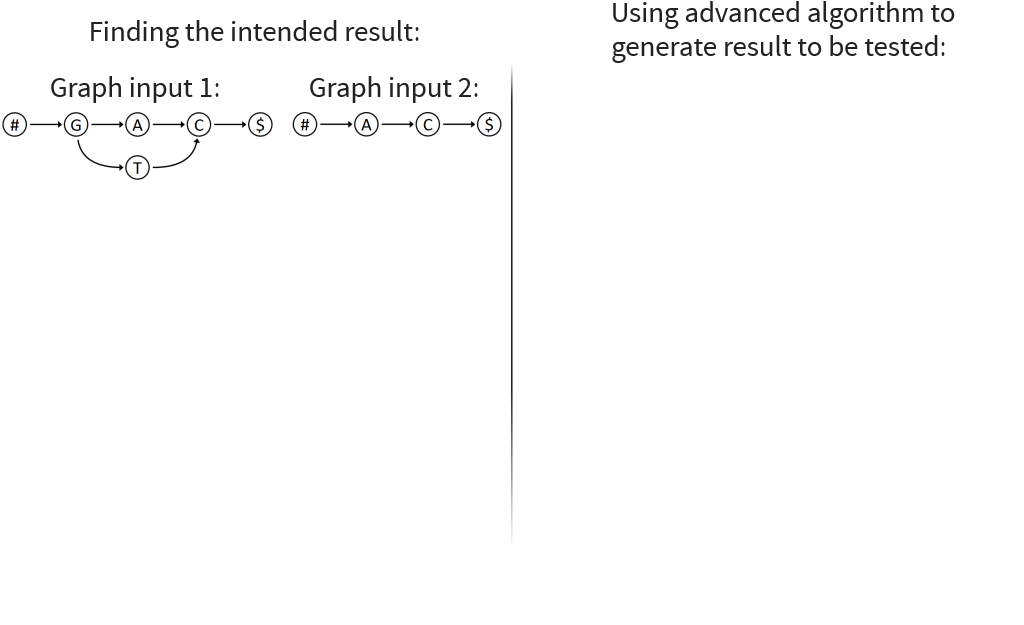
Long sequence to be transformed into graph with local variations
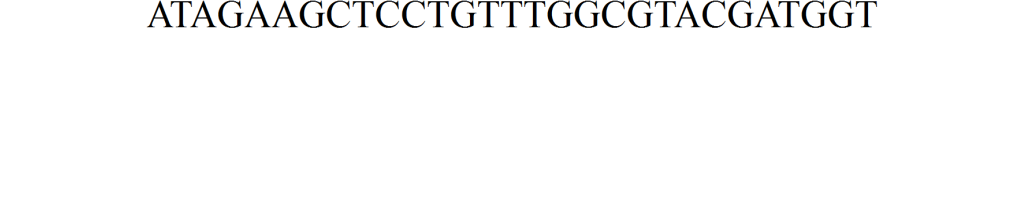
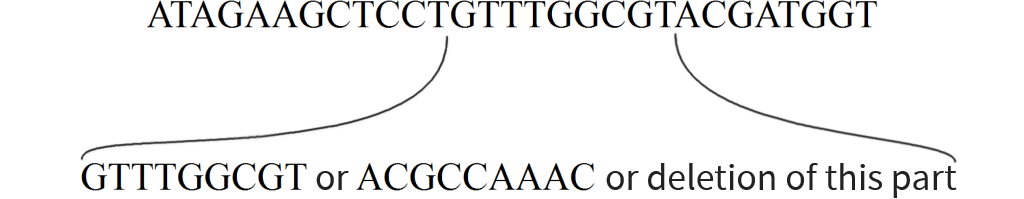



Start with sequential data
Want to add local variations
Split sequence up
Replace one sequence with graph
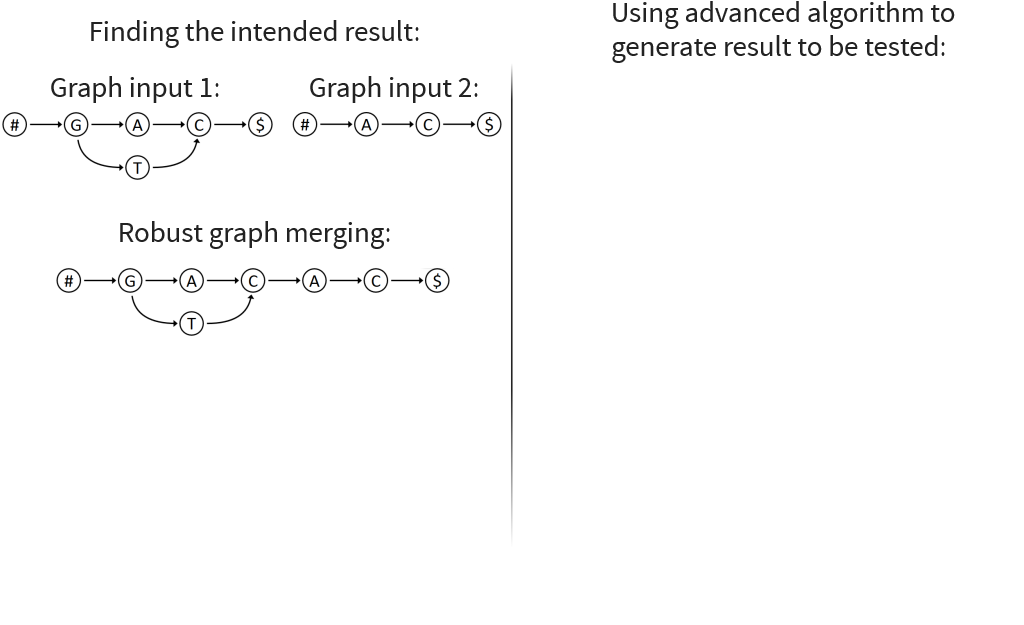
Merge graphs together

BWT is transformation of a string
(Burrows and Wheeler, 1994)
Together with suffix array allows us to quickly find patterns in the string
Can be used to find reads in reference

BWT can be extended to XBW (Ferragina et al., 2009)
XBW can encode trees instead of sequences
XBW can be further extended (Sirén et al., 2014)
Extended XBW can encode directed acyclic graphs
To use extended XBW, add specific start and end nodes
Ensure that graph is reverse deterministic
Make graph prefix-sorted
Some prefixes are ambiguous, so use node splitting
Continue with node splitting
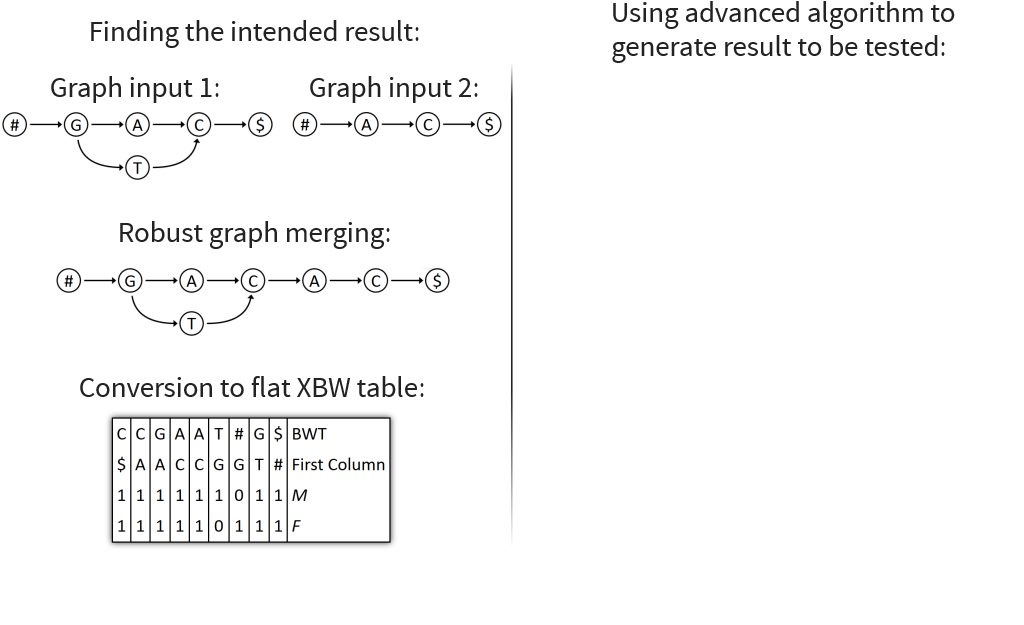
Graph can now be encoded using extended XBW

Represents a graph in a table
Has rows for BWT, prefixes, and bit-vectors M and F
Create XBW node table for given graph
Start with alphabetically sorted list of prefixes
Each column corresponds to exactly one node
Add BWT row with predecessor labels
Add rows with successor and predecessor amounts
Generated table now completely represents the graph
| G | G | G | C|G | G|T | # | G | T | T | T | C | C | C | $ | BWT |
| G | G | G | C|G | G|T | # | G | T | T | T | C | C | C | $ | BWT |
| $ | CG | CT | G$ | GCG | GCT | GG$ | GGC | GGG | TGC | TGGC | TGGG | TT | # | Prefix |
| 1 | 1 | 100 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | M |
| 1 | 1 | 1 | 10 | 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | F |

Similar to XBW node table
Prefixes not stored, making it smaller
Each row consists of flat sequential data
Create flat XBW table based on XBW node table
Only keep first letters of prefixes and rename row to “FC”
Copy FC value for each 0 in M
Flatten all cells
Pairs of columns correspond to edges
| G | G | G | C|G | G|T | # | G | T | T | T | C | C | C | $ | BWT |
| $ | CG | CTCCC | G$ | GCG | GCT | GG$ | GGC | GGG | TGC | TGGC | TGGG | TT | # | PrefixFC |
| 1 | 1 | 100 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | M |
| 1 | 1 | 1 | 10 | 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | F |
| G | G | G | C | G | G | T | # | G | T | T | T | C | C | C | $ | BWT |
| $ | C | C | C | C | G | G | G | G | G | G | T | T | T | T | # | FC |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | M |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | F |

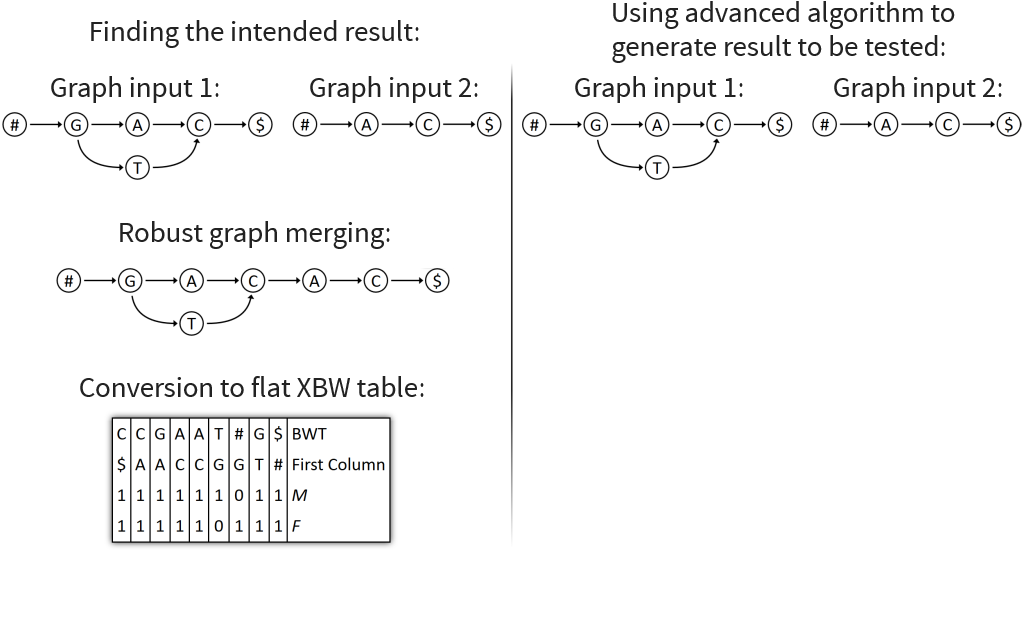
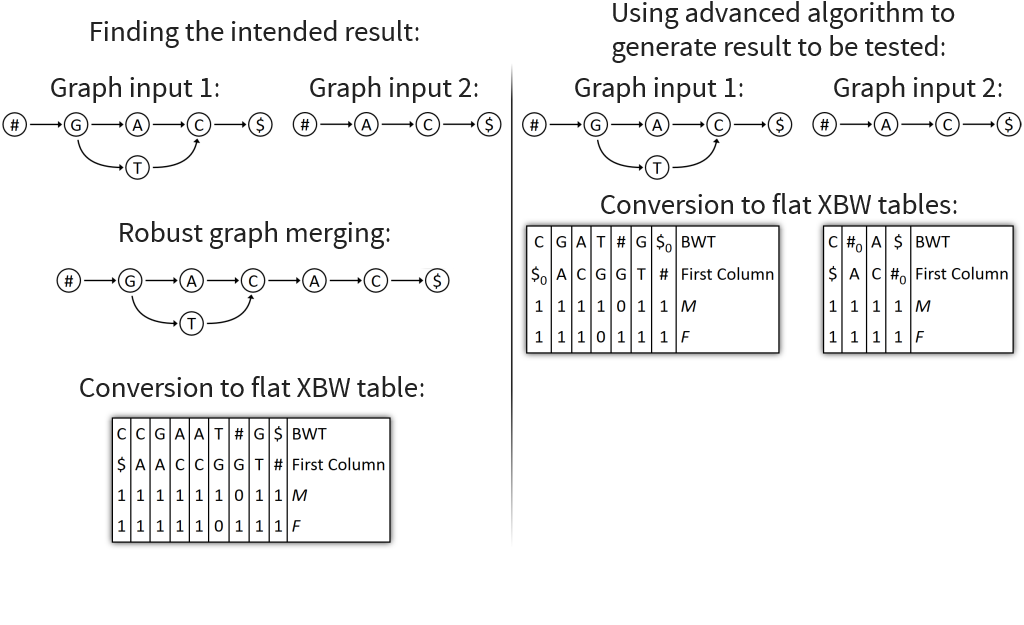
Implemented Graph Merging Library containing various algorithms for merging genomic graphs
Visualizes merging algorithms step by step

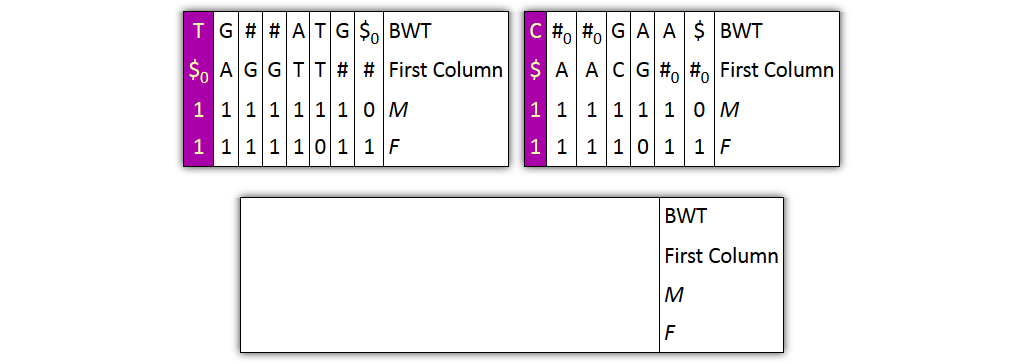
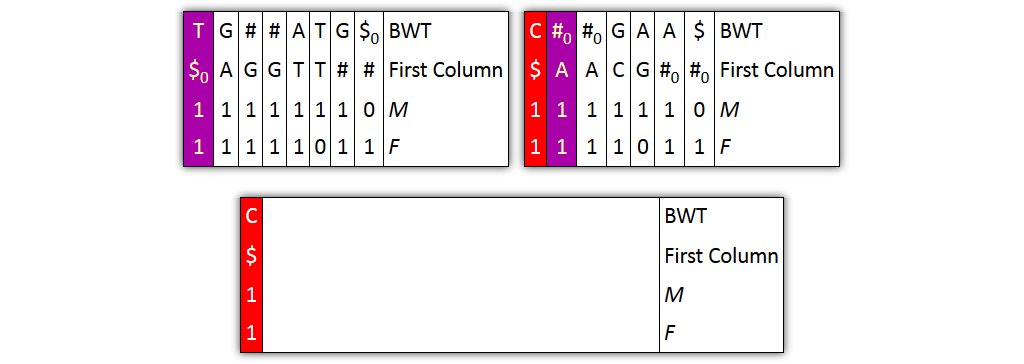
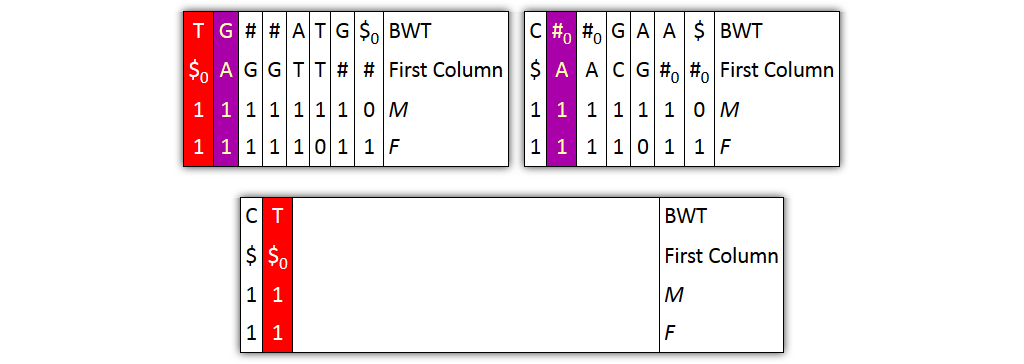
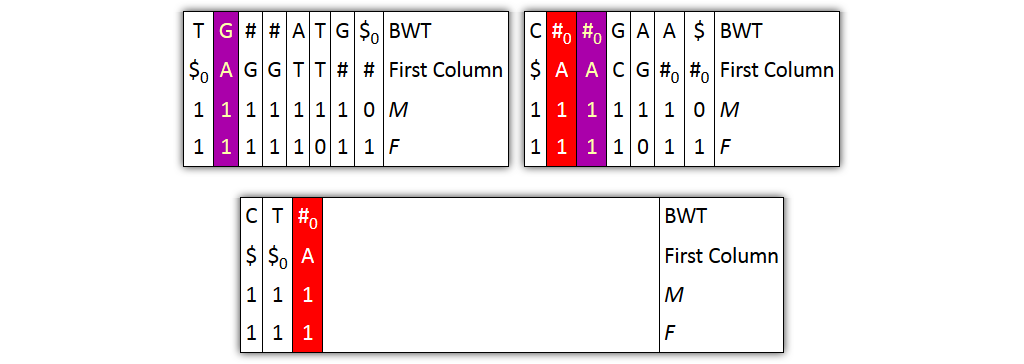
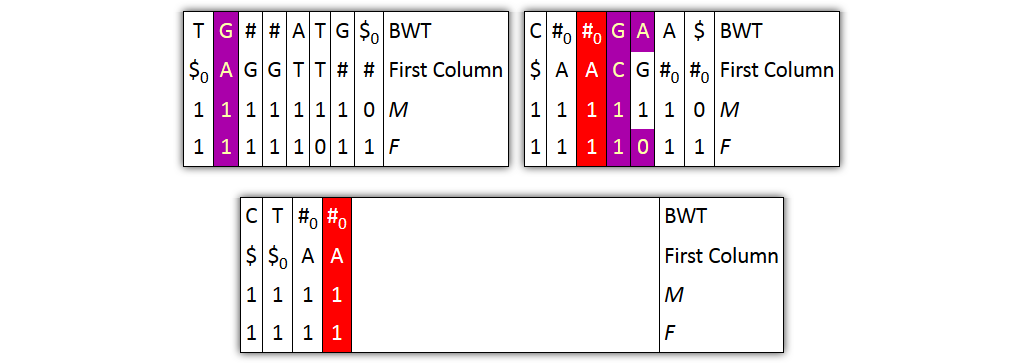
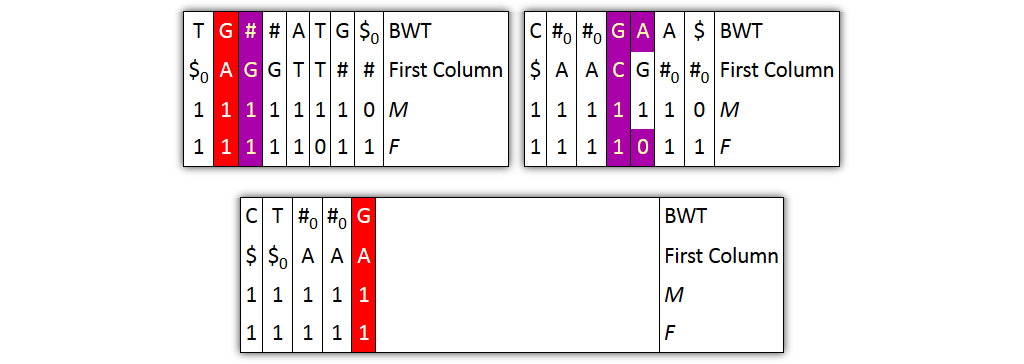
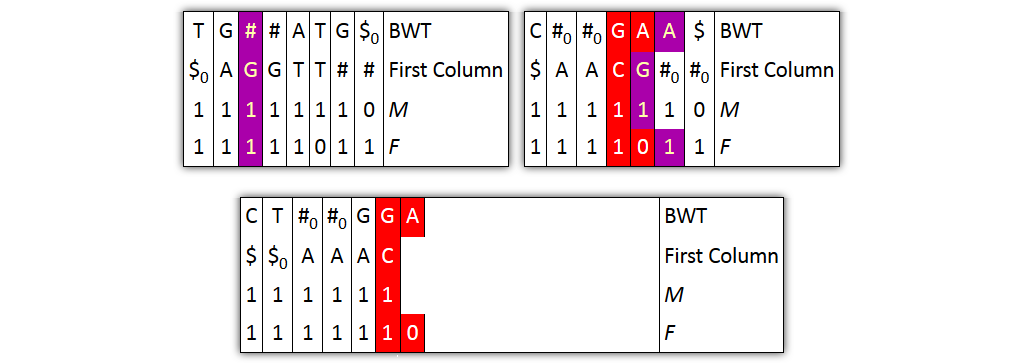
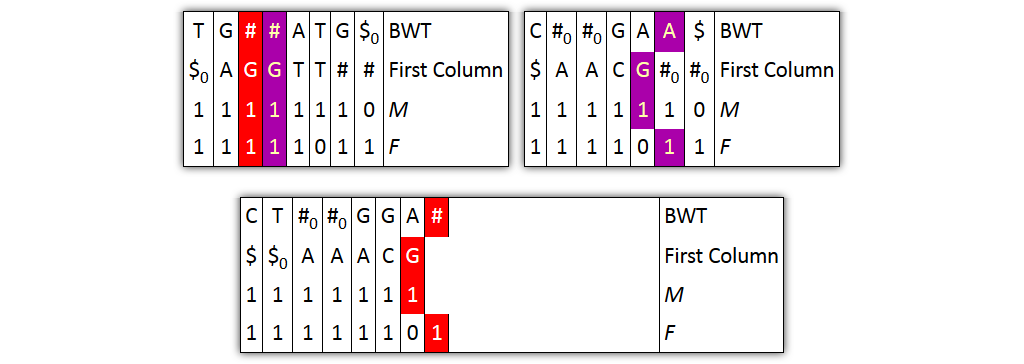
Core idea: put all columns from two node tables into one table, then sort columns alphabetically by prefixes
| T | G | # | A|T | G | $ | BWT |
| $ | A | G | T$ | TT | # | Prefix |
| 1 | 1 | 10 | 1 | 1 | 1 | M |
| 1 | 1 | 1 | 10 | 1 | 1 | F |
| C | # | G|A | A | $ | BWT |
| $ | A | C | G | # | Prefix |
| 1 | 10 | 1 | 1 | 1 | M |
| 1 | 1 | 10 | 1 | 1 | F |
| C | T | T | G | G|A | # | A | # | A|T | G | $ | BWT |
| $ | AC | AG | AT | C | GA | GC | GT | TA | TT | # | Prefix |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 | 1 | 10 | M |
| 1 | 1 | 1 | 1 | 10 | 1 | 1 | 1 | 10 | 1 | 1 | F |
| T | G | # | A|T | G | $ | C | # | G|A | A | $ | BWT |
| $ | A | G | T$ | TT | # | $ | A | C | G | # | Prefix |
| 1 | 1 | 10 | 1 | 1 | 1 | 1 | 10 | 1 | 1 | 1 | M |
| 1 | 1 | 1 | 10 | 1 | 1 | 1 | 1 | 10 | 1 | 1 | F |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | Origin |
Problem 1: both tables might share prefixes
→ Solution: make prefix-sorted by splitting nodes - can be done locally
Problem 2: column ordering in individual tables slightly different than in merged table
→ Solution: introduce aftersort array
| T | G | A|T | G | # | A | C | $ | BWT |
| $ | AA | AT | C | G | T$ | TA | # | Prefix |
| 1 | 1 | 1 | 1 | 10 | 1 | 1 | 1 | M |
| 1 | 1 | 10 | 1 | 1 | 1 | 1 | 1 | F |
| C | # | $ | BWT |
| $ | C | # | Prefix |
| 1 | 1 | 1 | M |
| 1 | 1 | 1 | F |
| C | G | A|T | T | G | # | C | A | $ | BWT |
| $ | AA | AT | C$ | CT | G | TA | TC | # | Prefix |
| 1 | 1 | 1 | 1 | 1 | 10 | 1 | 1 | 1 | M |
| 1 | 1 | 10 | 1 | 1 | 1 | 1 | 1 | 1 | F |
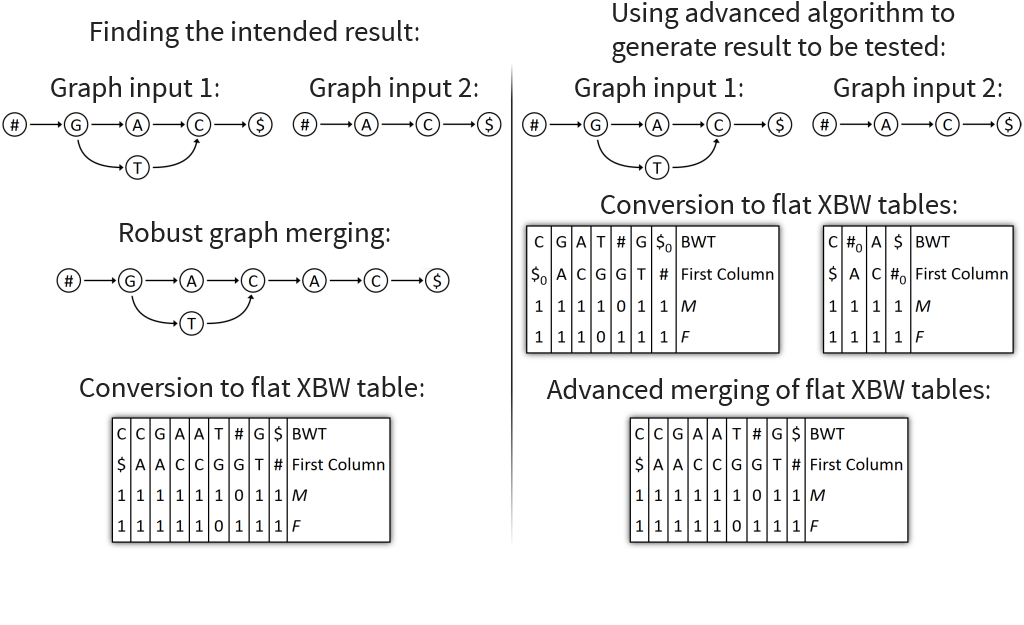
Problem 3: XBW node tables very big, as prefixes are stored entirely
→ Solution: merge flat XBW tables directly

Core idea: similarly to node table merging, put all columns into one table, alphabetically sorted by prefixes
Like with node table merging, aftersort array also used when ordering within first merged table changes
Problem 1: column pairs together, but not entire columns
→ Solution: merge BWT and F independently from FC and M
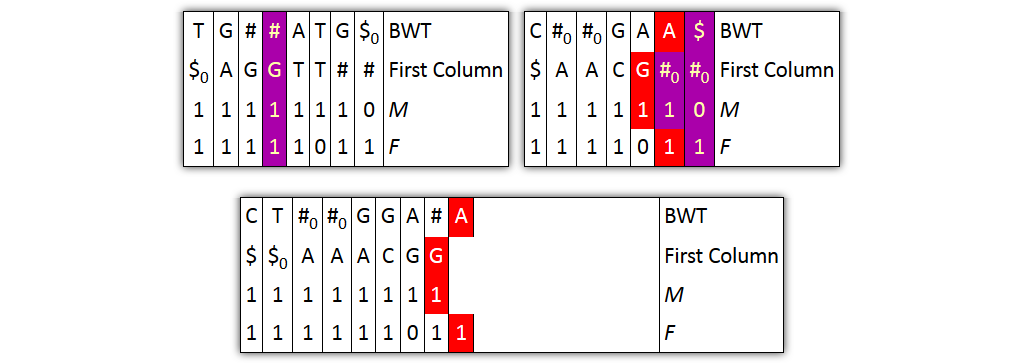
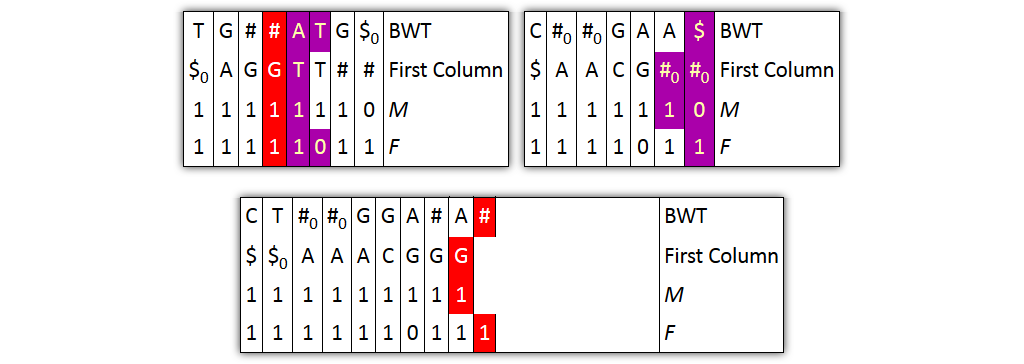
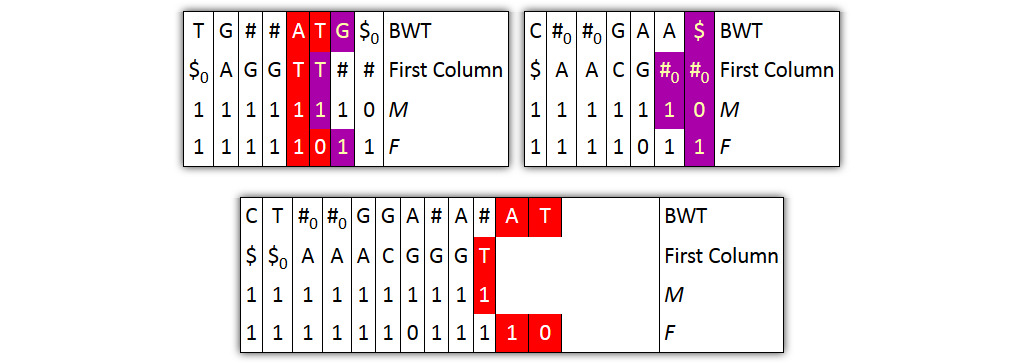
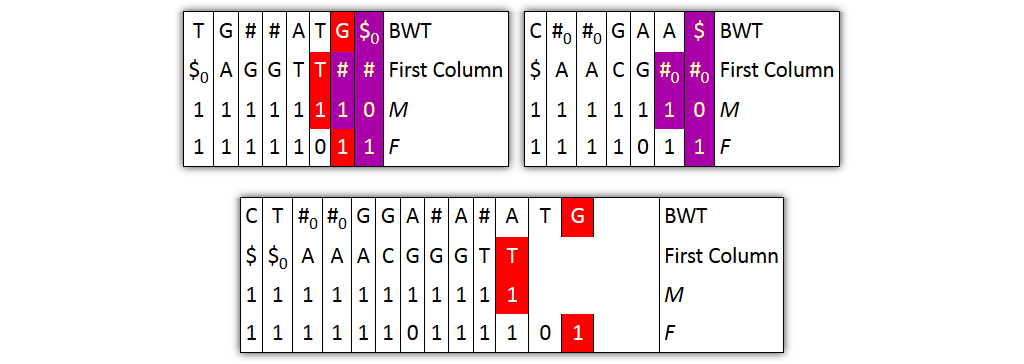
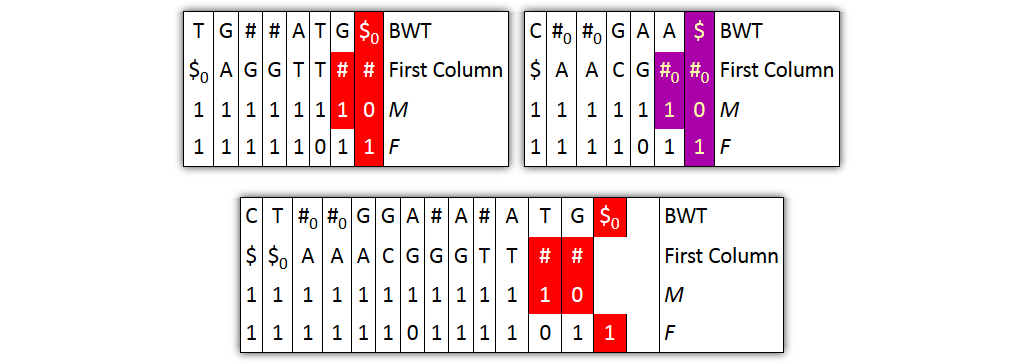
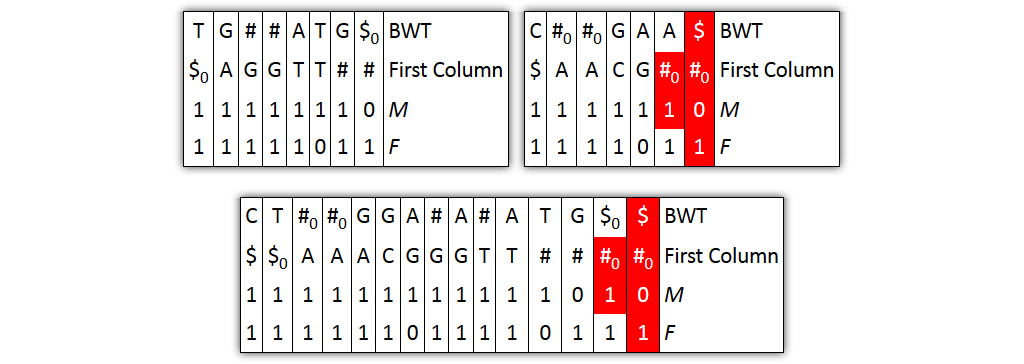
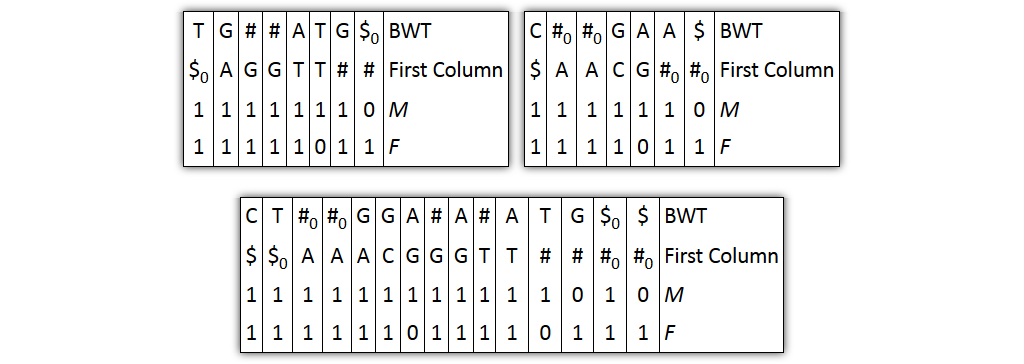
Problem 2: prefixes are not explicitly given
→ Solution: split nodes before joining columns
Problem 3: merging flat XBW tables can cause large amounts of node splitting
→ Large file size of merged graph
Also, merged graph needs to be constructed node for node
→ Direct opposite of what we wanted to achieve
→ Solution: fuse flat XBW tables instead of merging them

Core idea: keep tables separate and perform work on full graph by internally working on each table on its own
Problem: program working on fused table needs to keep track of interior tables
→ Solution: expanded navigation functions allow working with fused table without considering implementation details

Examine pattern finding in fused table in detail
Search for pattern “AC” in graph fused from two tables
Call highest-level navigation function find for pattern AC
Internally call LF for each fused table, here tables 0 and 1
First LF call for C on [0, 4], the entire interval in first table
(using absolute indexing)
Finds any C in the table's FC row, returns [2, 2]
Second LF call for A on interval [2, 2] in first table
Finds any A preceding nodes in the interval [2, 2]
A is found, and whole pattern has been stepped through, so that AC has been found in first table
Third and fourth LF call for C and A, now on second table
Overall result: [([1, 1]; 0), ([1, 1]; 1)]
| 0 | 1 | 2 | 3 | 4 | 5 | i |
| G | # | A | C | A | $ | BWT |
| $ | A | A | C | G | # | FC |
| 1 | 1 | 0 | 1 | 1 | 1 | M |
| 1 | 1 | 1 | 1 | 0 | 1 | F |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | i |
| C | T | G | A | T | # | $ | BWT |
| $ | A | C | G | T | T | # | FC |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | M |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | F |

Overall, merging possible, but complicated
Fusing in most cases preferable
→ Fusing also offers straightforward opportunities for parallelization
Through fusing, original problem of adding variations to long sequential data can be solved

Implementation of flat XBW table fusing in C++
Use fusing to generate entire human reference graph
Fusing as proposed here requires exactly one edge between fused graphs
→ Not very problematic, as focus is on long sequential data with local variations
Future work could focus on overcoming this requirement


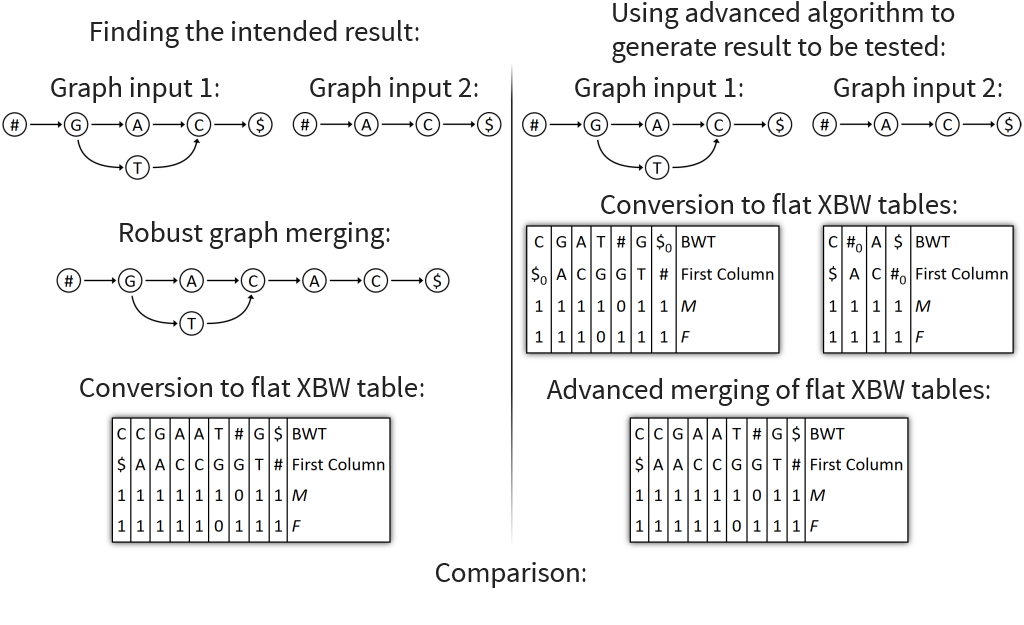
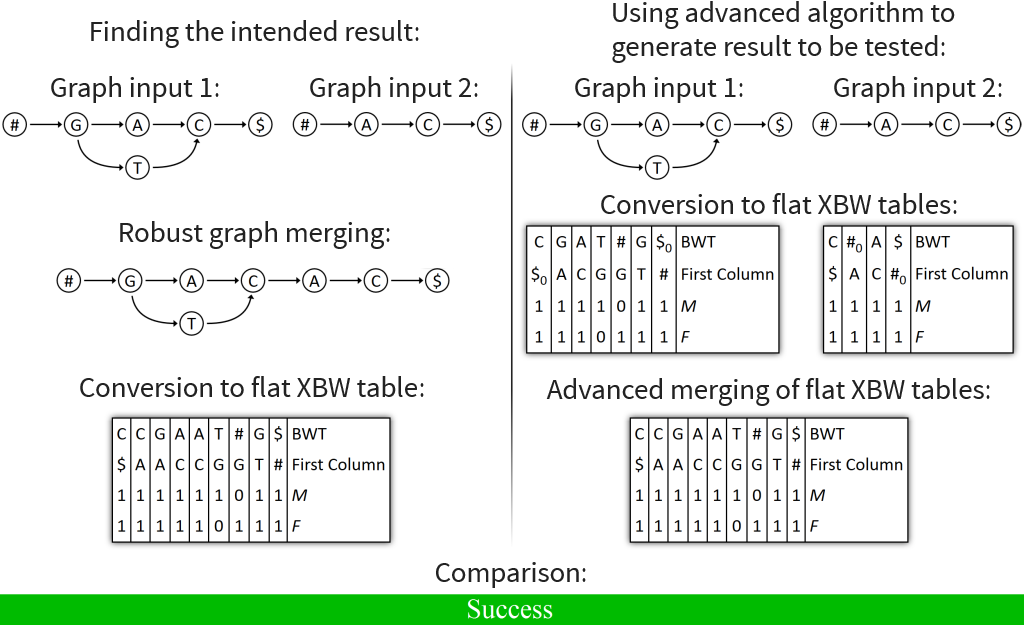
Automated tests performed for flat XBW merging and flat XBW fusing
Over 4000 merge tests with random input graphs executed
All tests successful